13の平方根とは、2乗したら13になる数。 よって±√13 (√13と−√13という意味) (2) 36の平方根とは、2乗したら36になる数。23/3/16 13的平方根是±√13, 用近似值表示: 13的平方根为±, 即±√13≈。 43 已赞过 已踩过 < 你对这个回答的评价是? 分享 新浪微博平方根とは? 平方根は、 「ある数 を2乗すると となるとき、その を の 平方根 という」 と定義されているものです。 文章を読むだけでは正直よくわかりませんね。 しかし、平方根の考え方自体には既に触れてきています。 正方形の面積と辺の長さの

センター数 A 追第1問 大学受験in北海道
13 の 平方根
13 の 平方根-数学Gアップシ-ト 3年第2章 平方根(13) 3年2章 No.13 -根号をふくむ式の加減の計算ができるようになろう①- p51 学習日 月 日 年 組 番 氏名 1 36+64は36+64と計算して よいでしょうか。平方根を含む式の計算について解説しています! 平方根では一番むずかしいところですね。 ぜひ最後まで御覧ください! 中学校 数学3年2章13 平方根



平方根 Qikeru 学びを楽しくわかりやすく
ルートとは?平方根の求め方を解説!分数や小数の場合はどうやる? 平方根、ルートの値を語呂合わせ!覚え方まとめ a√bの形に変形するやり方とは? 平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは?平方根を上手く表せないものが多くて困っちゃう そこでね! 昔の偉い人たちが ルート√という記号を使って平方根を表すことで この問題を解決していくことにしたんですね。 ちなみにルートの記号は 小数点以下の数が偶数なら 004の平方根 ⇒ \(\pm 02\)平方根計算機 オンラインの平方根計算機を使用して、入力した数値の平方根を見つけます。 平方根 数学では、数値xの平方根は、r 2 = xとなるような数値rです。 例えば、 1 5 2 = 25であるため、25の平方根は5です。 3 2の平方根はおよそです。 3
0 の平方根は 0 のみであり、平方根が一意に定まるのはこのときに限られる。 単位長と任意の長さ a が与えられたとき、 a の正の平方根の長さは定規とコンパスを用いて作図することができる。 定義 数 a に対して、 x 2 = a を満たす x を a の平方根という。平方根 へいほうこん square root 実数 a に対して,x 2 =a を満たす実数 x を a の平方根と呼ぶ。 a が正数のとき a の平方根は正数であるものと負数であるものの二つが存在し,このうち正の方を√a で表す。 0の平方根は 0である。たとえば,√2=,√3=であり,これらは12/4/08 展开全部13开算术平方根≈ 3 已赞过 已踩过 < 你对这个回答的评价是? 分享 新浪微博 QQ空间 举报 收起
在數學中,一個數 的平方根 指的是滿足 = 的數,即平方結果等於 的數。 例如,4和4都是16的平方根,因为 = = 。 任意非負實數 都有唯一的非負平方根,称为算术平方根或主平方根(英語: principal square root ),記為 ,其中的符号√称作根号。 例如,9的算术平方根为3,记作 = ,因为 = = 并且3非28/3/18 つまり、±13は169の平方根です。 ですから、±13でないことはわかります。 1人 がナイス!2(1) 13- 6 (2) 3 3 P111 4 (x ,n)=(2,5),(10,11) 18 通り 解説 どれか1 つ,色を固定して考えるとよい。 1 に赤を使うとする。次に1 のとなりの2,3 に 使う色について考える。2,3 に使える色は2 つ とも同じか別々の色のどちらかである。




高校数学 数 13 ルート シリーズ 有理化編 Youtube




数学の勉強のコツ 中3平方根編 学習塾コンパス 学習塾compass
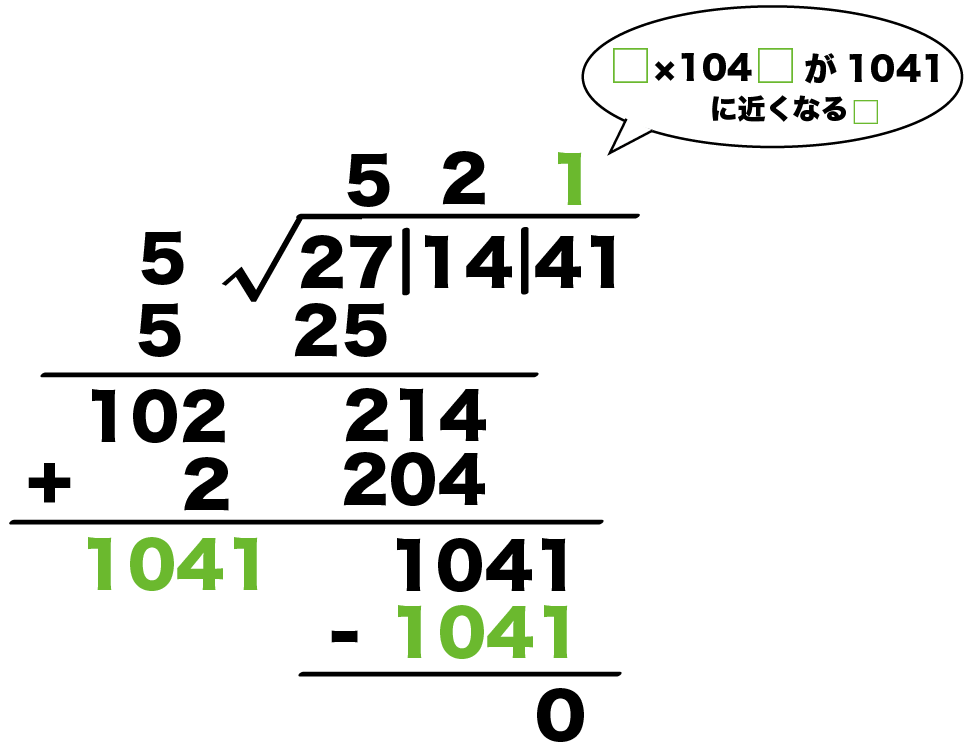
19/7/16 の平方根はそのうえの数字の「521」だよ。 やったね。 13ステップは長すぎるぜ^^ まとめ:筆算をつかった平方根の求め方は辛い 平方根の求め方に筆算をつかうと、 でかい数の平方根を求めるとき; 1 の平方根 =1 2 の平方根 = 3 の平方根平方根 有理数と無理数 1 次の(あ)~(お)にあてはまる言葉を、①~⑤の中から選びなさい。 数 正の整数( ) 0 2 次の①~⑤の中で、無理数であるものを選びなさい。 324 ① 自然数 ② 有理数 ③ 分数 ④ 無理数 ⑤ 負の整数




中学3年数学 平方根 根号を含む式の計算 2確認問題3 あんのん塾




数学わかる教え方学び方 13 測りきれない数 無理数 平方根 堀井 洋子 遠山 啓 銀林 浩 本 通販 Amazon
平方根計算法 実行結果 正整数 12の平方根の整数部 = 3 正整数 1234の平方根の整数部 = 35 正整数 の平方根の整数部 = 351 正整数 の平方根の整数部 = 3513 ok 改良 1234の平方根を求める。 1234を2桁ずつに分ける。 ①12の平方根を求める。 0 < 12 135 < 12 < 1357動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru平方根の覚え方 2、3、5などの平方根の値は暗記すると便利です。平方根の値は、物理学や工学で使うからです。語呂合わせを下記に示します。 上記の平方根は、最低限覚えるべきでしょう。 平方根の公式と問題 平方根の公式を下記に示します。




平方根を簡単にする 3つの方法 Wikihow



2
表3のように中学校第3学年の「平方根」の単元の 指導計画を立て,第3時と第13時で平方根トランプを 用いたババ抜きやジジ抜きを実施する。「平方根」の 学習は,内容が抽象的でイメージしづらく ,生徒に とって理解しづらい単元である。15/6/19 素早く、ルートの中の数字を小さくしたり、整数に直すトレーニング教材です! 目標は秒です! 学年 中学3年生, 単元 平方根,根号をふくむ式の計算, キーワード 平方根,ルート第3学年 2 平方根 Title Taro3年平方根プリント613jtd Author tsukahara Created Date PM




映像授業で勉強を応援 Npo法人eboard イーボード
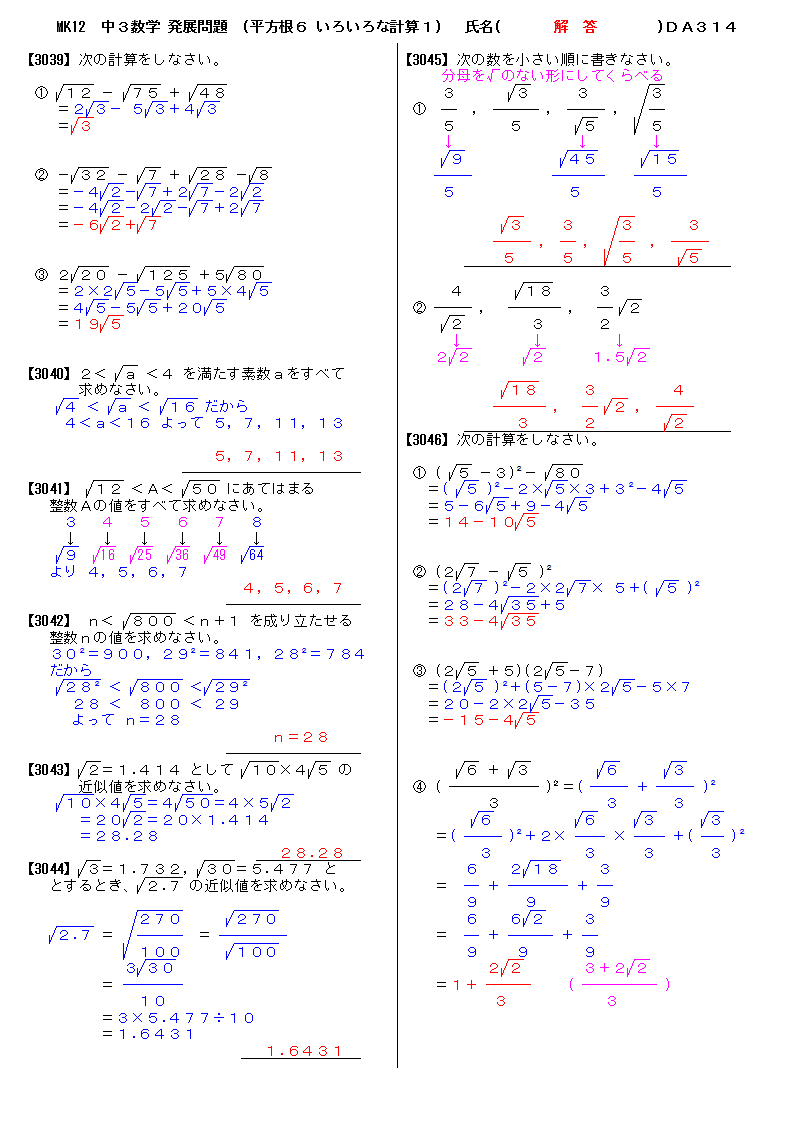



無料 中3数学 発展 応用問題 解答プリント 314 平方根6 いろいろな計算1
平方根が整数となるnの値・・・(平方根をまだ習っていない方は,平方根の勉強を先にして下さい。) → 印刷用PDF 最小となるのは8n=21よりn=13用于求解32位数据中从bit31开始的0的个数。 平方根函数用到__sqrtf指令。 用于求解浮点数的平方根,用户可以直接调用此指令,求平方根非常方便。 133 三角函数(Cosine) 三角函数cosine的计算是通过查表并配合直线解答① 平方根 2② 2 ③ − (②と③は順不同) ④ 0 解説 例えば,2 乗して 25になる数が25の平方根なので,5だけ でなく−5もはいる。0 の平方根は0 だけであるが,それ以外 の場合は±の2 通りがある。また7 の平方根のように,整数・ 分数・小数で表すことができないものは,± 7 (プラス
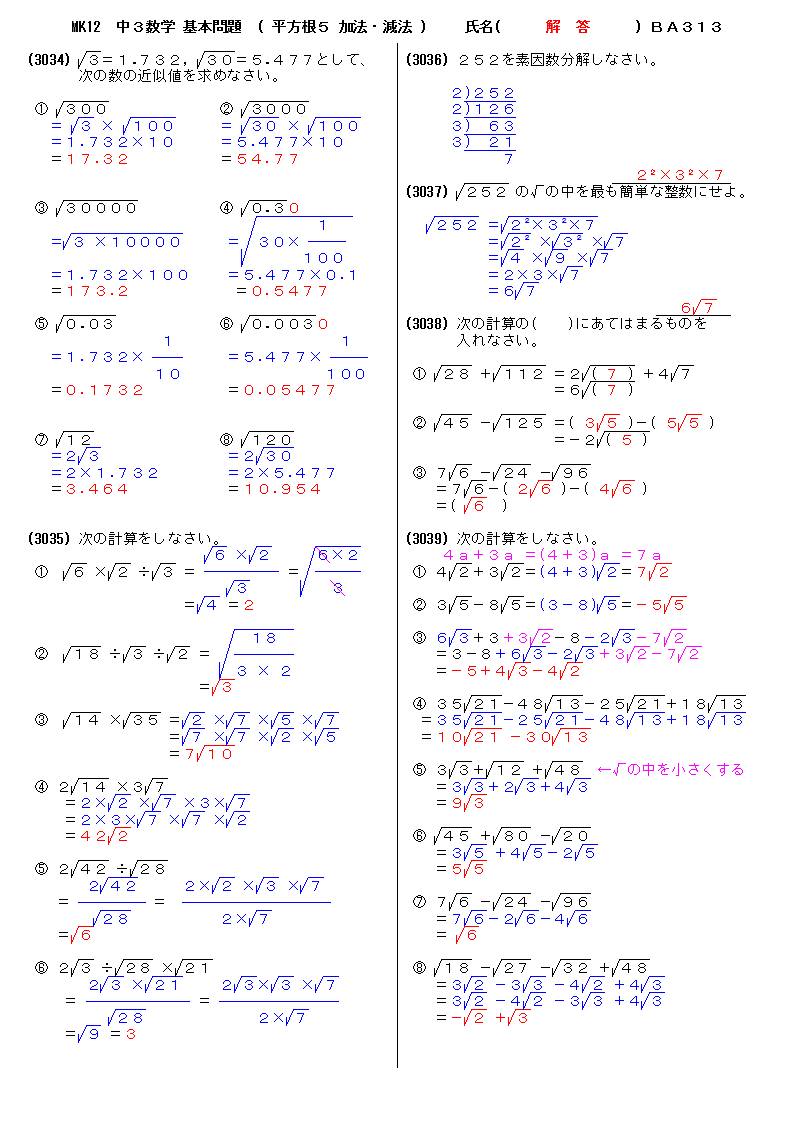



無料 中3数学 基本問題 解答プリント 313 平方根5 加法 減法



2
平方根1_平方根を求める x 2 =A のとき xをAの 平方根 という。 正の数には平方根が2つ,0の平方根は0だけで,負の数には平方根はない, 解説動画 ≫ 次の数の平方根を求めよ。 25 1 4 6 ① 2乗して25になる数は 5と5なので 答 ±5 ② 2乗して 1 4 になるのは 1 2 と1 2 な25/8/21 15.平方根とは? (1) 言葉の意味からいきます。 「平方根」とは・・・? 「平方」は「2乗」のこと。面積の単位「平方cm」でおなじみだ。 「根は「根(ね)」なのだが,数学的には「根(こん),何かの元になるもの」という意味合いで使われる。 つまり,平方根とは,「2乗するときの元计算整方的平方根很容易,但计算其他的平方根 非常困难。 例子: √10 是什么? 我们来看看: 3 × 3 = 9, 4 × 4 = 16,所以我们可以猜到答案是在 3 和 4 之间。
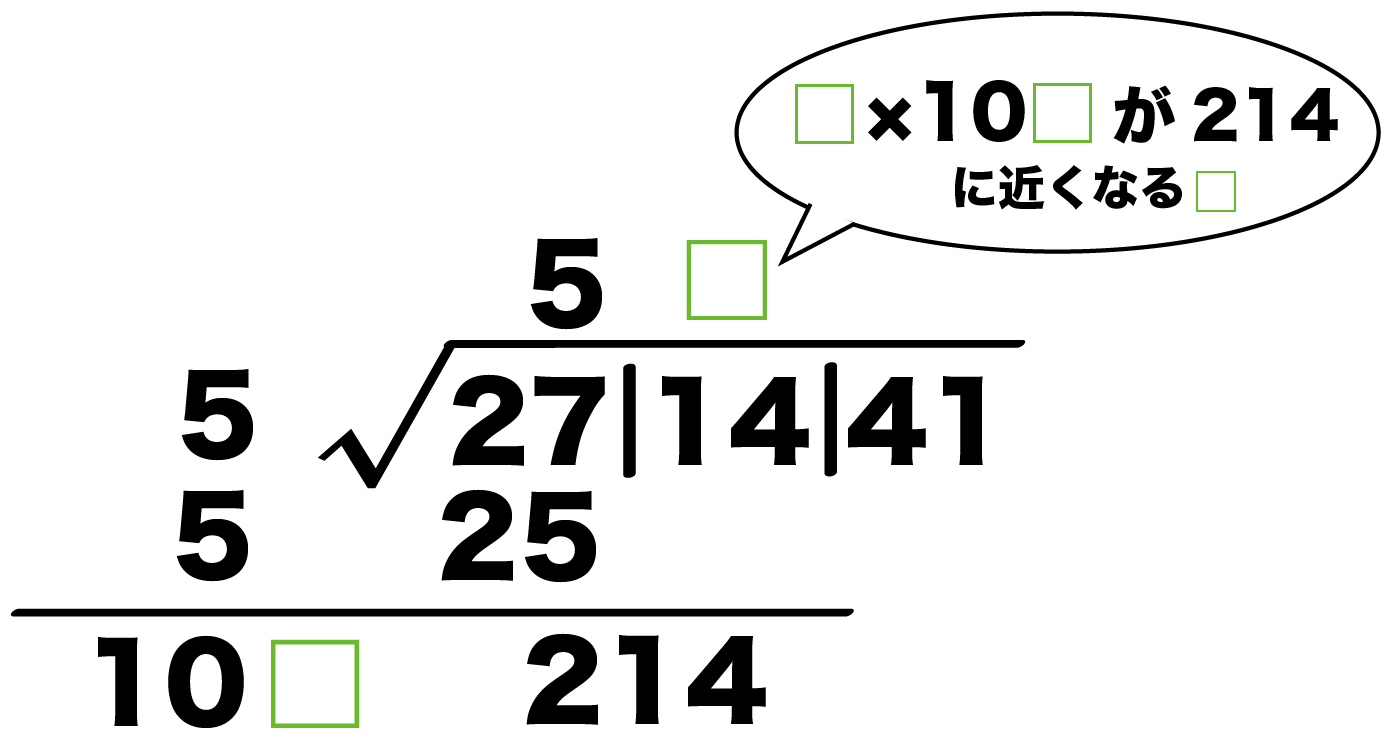



開平法 筆算で計算する平方根の求め方の13ステップ Qikeru 学びを楽しくわかりやすく




無料プリント 平方根のa Bの形にする問題 ランダムで作ります スタディーランナップ
22/2/11 21世纪教育网为您提供资料131平方根(二)下载,简介(131平方根(二)rar一、基础过关1.下列说法正确的是( ) A.2是4的平方根; B.2是(2)2的算术平方根 C.(2)2的平方根是2; D.8的平方根是±22.若一个数的平方根等于它本身,那么这个数一定是( ) A.正数 B.负数 )3/3時 ねらい ・ 正方形の面積と1辺の長さの関係から、新しい数を見つけることができ、平方根の大小関係について理解する。 ・ 平方根の大小関係を不等号を使って表すことができる。 段階 学習活動 数学的活動を通した指導のポイント ( は数学13の平方根: 14の平方根: 15の平方根: 16の平方根:4 17の平方根: 18の平方根: 19の平方根: の平方根: 21の平方根:



コンピュータさん13は素数ですか オンライン家庭教師 九大パル



こうゆう問題系はどのように解いたらいいですか 平方根やルートな Yahoo 知恵袋
平方根 √ 、立方根 3√ 、累乗根 n√ を計算します。平方インチ から 平方センチメートル表 Start Increments 値を増加: 1000 値を増加: 100 値を増加: 値を増加: 10 値を増加: 5 値を増加: 2 値を増加: 1 値を増加: 01 値を増加: 001 値を増加: 0001 分数: 1/64 分数: 1/32 分数: 1/16 分数: 1/8 分数: 1/4 分数: 1/230/4/ 「中3 数学 平方根の利用」 についてです。(問題)大きい円の中に,半径5cmの小さい円が4個ぴったりと入っている。その4個の円の中心は正方形の頂点になっている。(1)は分かったのですが、(2)が解説を見てもどうしても分かりません。解説が出




平方根のおよその値の求め方とその利用 わかるようになる高校数学



平方根でわからないところがあります 13番は0 5になってしまうのです Yahoo 知恵袋
数a 的n(n为自然数)次方根指的是n方幂等于a的数,也就是适合b的n次方等于a的数b。例如16的4次方根有2和-2。一个数的2 次方根称为平方根; 1 3次方根称为立方根。各次方根统称为方根。求一个指定的数的方根的运算称为开方。中三数学13 平方根の利用平方根の展開とややこしい最小の自然数nをやっていきます! 解説・講座 ヤソニキチャンネルを見ていただきありがとうございます!勉強はしたくないけど、しないといけな開平法の原理 与えられた正の数の正の平方根の小数表示を求めるために、ここではまず漸化式を立てて、一般的な求値法を求める。 そして、求値の明確化のために、開平法と呼ばれる筆算の原理を導出する。 以下は十進法表示の場合だが、他の位取り記数法でも同様な計算で求められる。




平方根 の問題のわからないを5分で解決 映像授業のtry It トライイット



Www Pref Oita Jp Uploaded Attachment Pdf
N=13,14,15,16,17 ※ 「自然数」とは「正の整数」のことですが、この問題ではnは正の数しかありませんので (根号の中にあり、√が正だから0でない)、問題文が「・・・整数n・・・」となっていても同じことになります。 (3) を満たす整数nを求めなさい。




平方根 A B の形に変形するやり方とは 問題を使って徹底解説 数スタ



Sukinakazu Net Heihoukonn Heihoukonn Pdf




世界一わかりやすい数学問題集中3 2章 平方根




平方根




無料 中3数学 基本解説 解答プリント 309 平方根1 意味
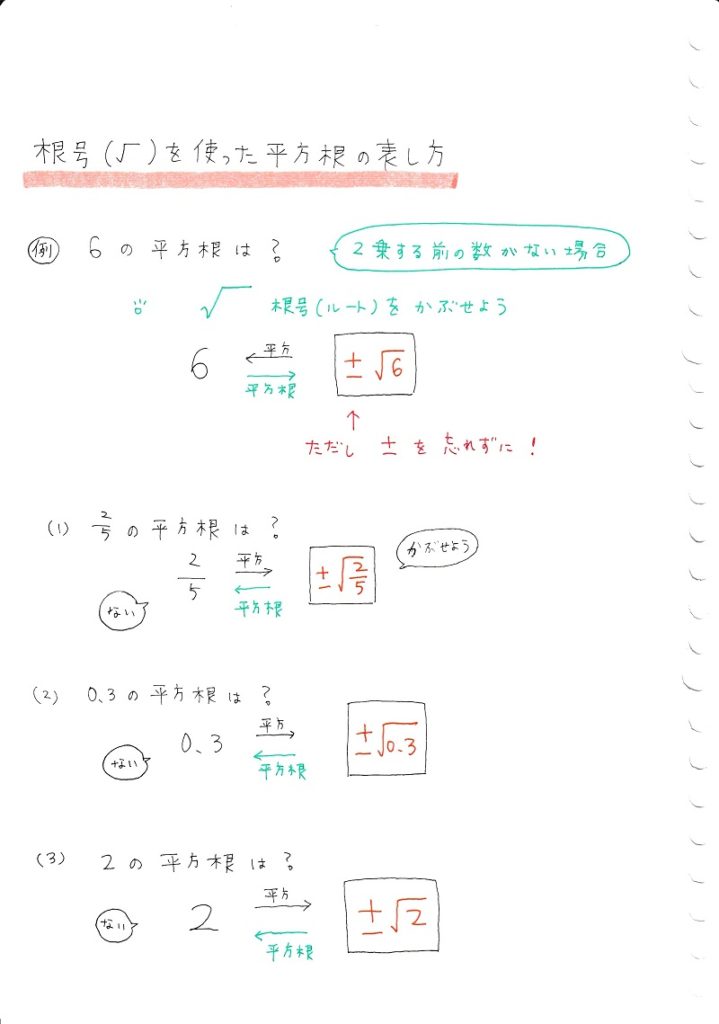



中学数学 平方根 ママ塾ノート




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




センター数 A 追第1問 大学受験in北海道




平方根の掛け算 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校




かっこのルートを二乗する問題 を外すだけなので簡単 中学や高校の数学の計算問題



Kumanichi Com Assets Image Examination 18 Sugaku 25 Pdf
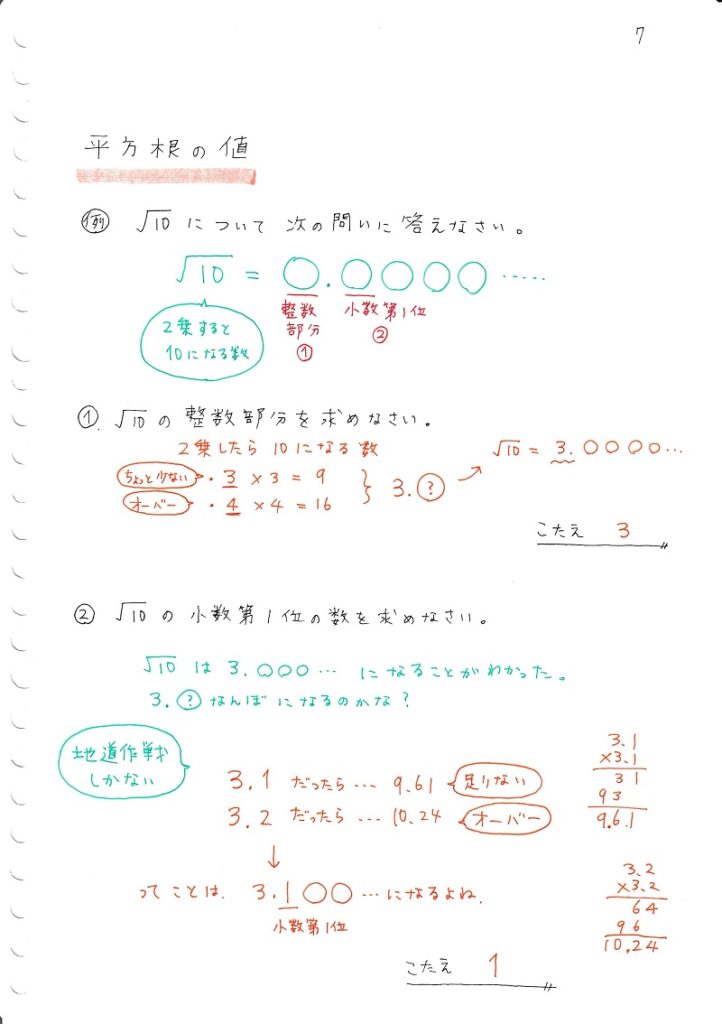



中学数学 平方根 ママ塾ノート




教科書tv 中3数学



3 37第2章平方根の計算 根号を含む式の除法 ニュージーランド短期留学ダイアリー




Css3 Columns Is Not Support Issue 41 Wkhtmltopdf Wkhtmltopdf Github




中3 三年数学 平方根 授業ノート 中学生 数学のノート Clear




数学の一問一答 平方根 勿忘荘




数学 中3 15 平方根 Youtube



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




中3数学13 平方根 Youtube
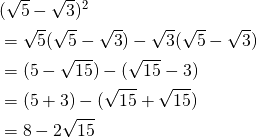



ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




Amazon 13年歳の誕生日おかしい数学の平方根 トレーナー トレーナー パーカー 通販
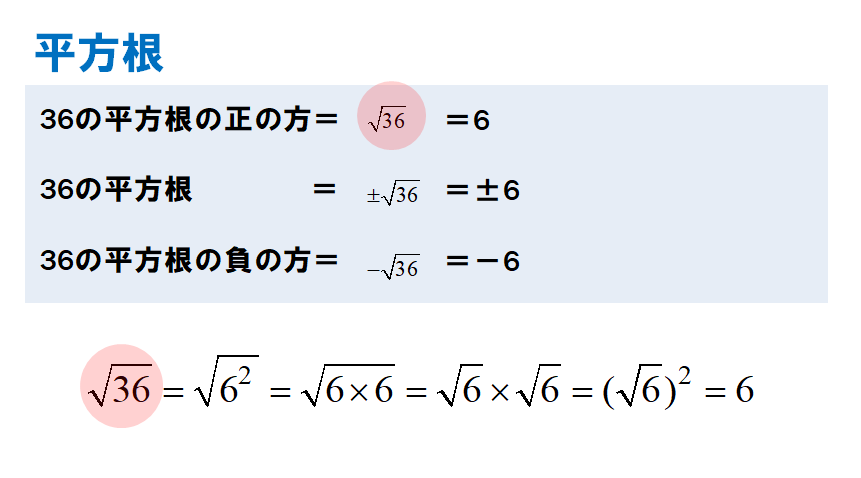



中3数学 平方根の性質の定期テスト対策問題 Examee



中学数学なら数学わかルート 無料動画で学ぶ




平方根 加減法 無料で使える中学学習プリント




中3 平方根です Clear




平方根の計算 数学の要点まとめ 練習問題一覧




日本ケイデンス デザイン システムズ The Sound Of Cadence Online




世界一わかりやすい数学問題集中3 2章 平方根




平方根の整数部分がわかりません 教えてください Clear
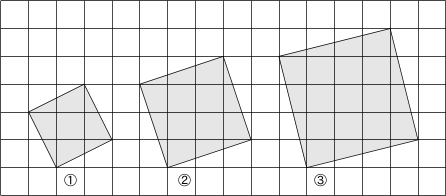



平方根応用 図形 1 2 3 解説




問13を教えてください 答えも込みで Clear




根号 の意味と覚え方 ルートは 何のために作られた 三重の個人契約家庭教師




平方根 Youtube




中三数学13 平方根の利用 平方根の展開とややこしい最小の自然数nをやっていきます ニコニコ動画




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




平方根 Qikeru 学びを楽しくわかりやすく




平方根 とは 根号の意味や性質 値の求め方について 数学fun
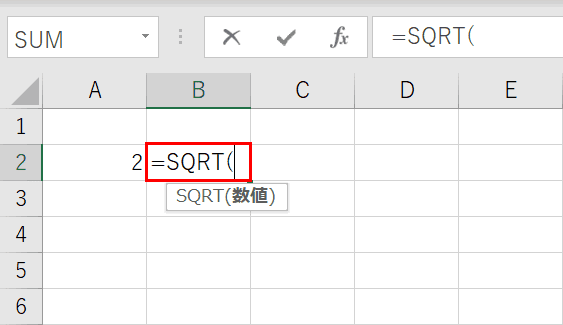



エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack




Tokusin P 13 8 34 3 05という平方根を使わない解答があることに気づいた
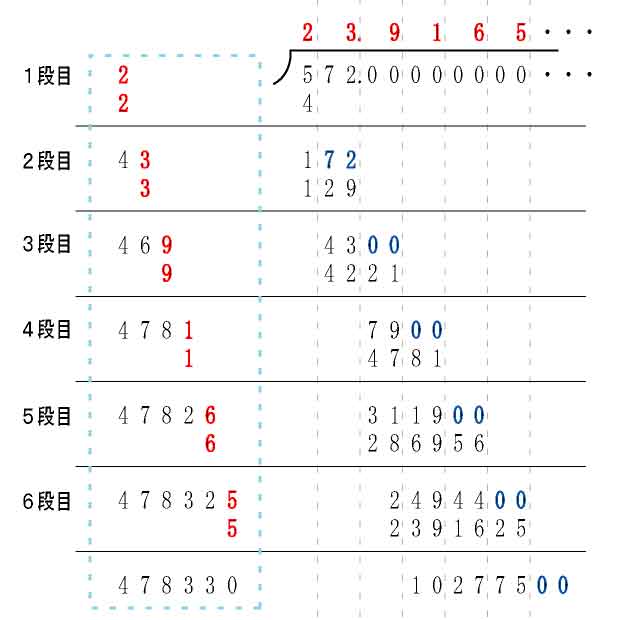



開平方 平方根の求め方 時じくの香の木の実




05 号 拡大体平方根算出装置 拡大体平方根算出方法 拡大体平方根算出プログラム及びそのプログラムを記録した記録媒体 Astamuse




中三数学13 平方根の利用 平方根の展開とややこしい最小の自然数nをやっていきます ニコニコ動画




平方根の問題の解き方 6パターン 数学fun



8 平方根カルタ 初級編 タコちゃんイカちゃん いらっしゃ い 楽天ブログ




機械学習のための数学基礎の基礎まとめ 平方根と累乗根 釣りキチエンジニアのブログ




平方根 Youtube




6的13平方根是多少 搜狗搜索



3 45第2章平方根の応用 平方根の性質を使った問題 フロントエンドなブログ




3の平方根 Wikipedia




中3数学 平方根 13 中学数学高校数学個別指導in山形市 数専ゼミ




しょうちゃん 公式ブログ この計算できますか No 115 平方根 工夫して計算 Powered By Line




平方根 そもそも 平方根 ってなんやねん 中3向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ
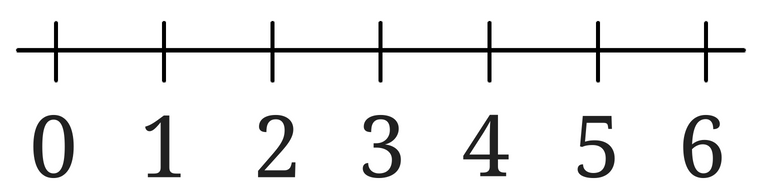



平方根の近似値を求めるにはどんな考え方をするの 語呂合わせを使った覚え方は さびねこ中学校




13 Sqrt 14 Sqrt Sqrtpractice1 C 1 2



Www Tsumugi Ne Jp Pdf Step3 3 2 1 Pdf
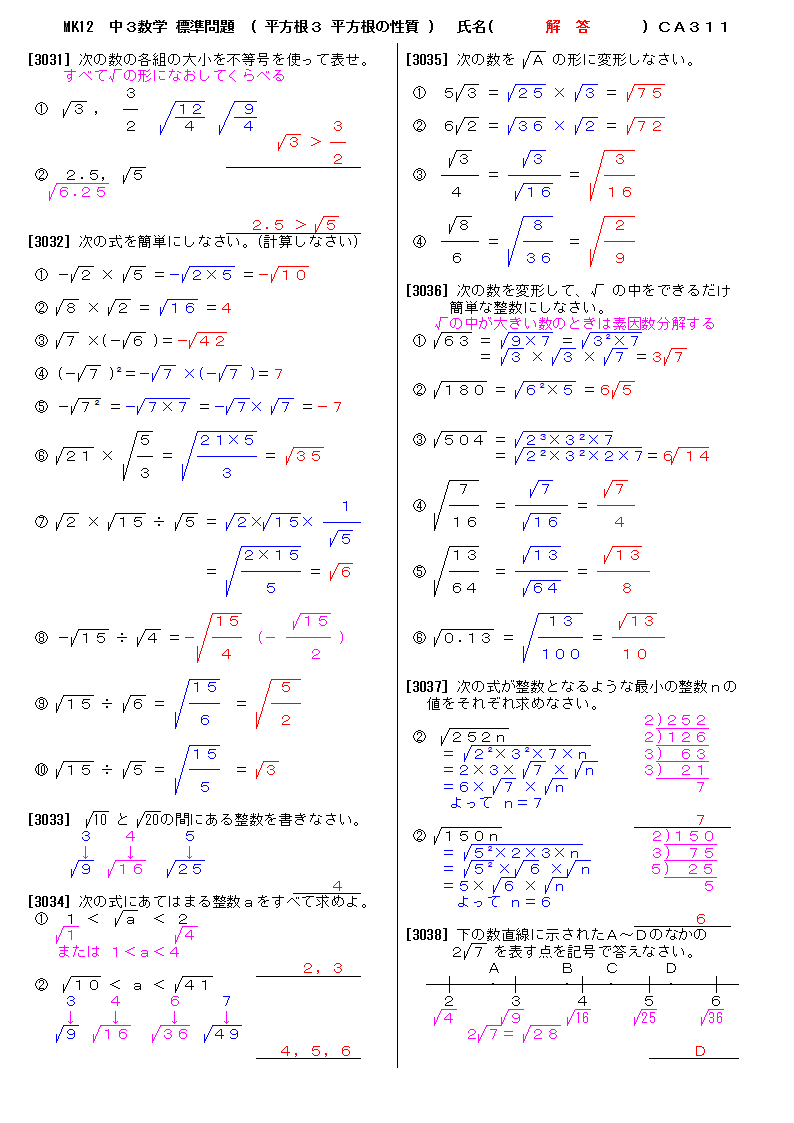



無料 中3数学 標準問題 解答プリント 311 平方根3 平方根の性質




京都文教中学高等学校 10月23日 高校入試関連情報 本校を受験する しないに関わらず 基礎学力の向上と高校受験サ Facebook




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ



2
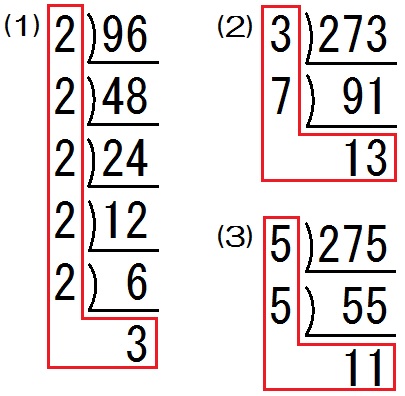



中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算




中3 平方根1 中学数学の勉強に




平方根 ルート の計算をおぼえよう しろカスと学ぶ中学数学 理科




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ



平方根の問題を教えてもらいたいです 問13をお願いします Yahoo 知恵袋
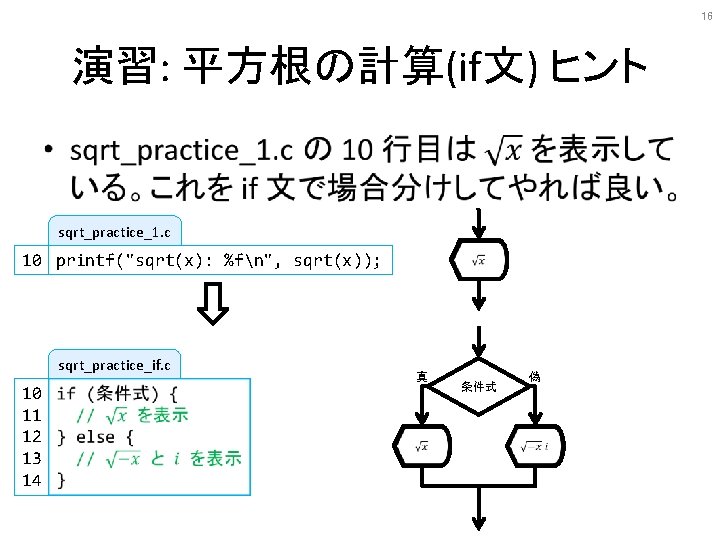



13 Sqrt 14 Sqrt Sqrtpractice1 C 1 2




中3 平方根 特別編 正誤問題 中学数学の勉強に




数学わかる教え方学び方 13 測りきれない数 無理数 平方根 堀井 洋子 遠山 啓 銀林 浩 本 通販 Amazon



2




ルート 平方根 二乗根 計算機 かんたん計算機




開平法 筆算で計算する平方根の求め方の13ステップ Qikeru 学びを楽しくわかりやすく




大人の学び直し 中学数学 平方根2 80まで原石



1




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ




センター数 A 追第1問 大学受験in北海道



平方根の問題なのですが13の正の平方根の答えは 13だと思っているのですが Yahoo 知恵袋




平方根の乗除計算 チーム エン



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




02 号 平方根の逆数計算方法 計算回路 及びプログラム Astamuse
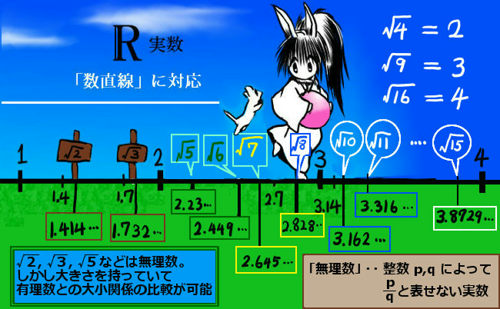



平方根って何だろう 理数系無料オンライン学習 Kori



0 件のコメント:
コメントを投稿