三角関数の積分:$1}{sin x},\ {1}{cos x$の積分 通常は別解1が正攻法とされ,\ 問題集などでもその解法のみが示される 問題が単純な割に微分形接触型,\ 部分分数分解,\ 1次式置換型などが総重積分の計算方法と例題3問 レベル 大学数学 解析 更新日時 この記事では重積分の計算方法を,例題を通じて解説します。 重積分の厳密な定義や順序交換の条件などは専門書を読んで下さい。 なお,二重積分のみ扱います。 三重積分なども分数関数の積分の分類 分数の形をした関数の積分はいくつかパターンがある。特に分母分子がともに整式(\(\small{ \ n \ }\)次式の形)になっている関数で、分母分子の次数や形によって解き方が異なるから、今回はそのパターンについて考えていこう。
分数関数の不定積分
分数 積分 ルート
分数 積分 ルート-(A) 一般に,分数関数は(分子)÷(分母)の割り算によって商と余りに分けると,「 分子の次数<分母の次数の形 」 (数研の参考書で「分数式は富士の山」と呼ばれるもの) に変形することができる.この変形により,分数関数の不定積分を求めるときは,分子の次数が分母の次数よりも低い形だけを考えればよいことになる.不定積分(まとめ2) 不定積分の漸化式 → 携帯版は別頁 == 分数関数の不定積分 == 《解説》 分数関数の不定積分については,次の流れに沿って処理すると分かりやすくなります. (1の詳細) 分子の次数が分母よりも大きいとき(又は等しいとき




平方根内が2次式である関数の不定積分 身勝手な主張
積分です。 これlogの分数になるときはマイナスのときだと思うのですが、どうして足し算 Clear 積分です。 これlogの分数になるときはマイナスのときだと思うのですが、どうして足し算なのに分数になっているのでしょうか? お願い致しますm (_ _)m累次積分 次に,重積分の値を求める際に,具体的にどのような計算をするかを見ていきましょう。下の図を見てください。 まず, \(x\) 軸方向には固定して, \(y\) の向きに分割した長方形上にできる四角柱の体積を加えます。 分数に関する不定積分は、基本xのp乗の不定積分で見た、\ \int \dfrac{1}{x} dx=\logxC \が使えそうです。 しかし、例題の不定積分は、 $\logx(x1)C$ ではありません。微分してみると、\ \frac{2x1}{x(x1)} \となってしまいます。
ルートxを含む式の積分公式 具体例で学ぶ数学 > 微積分 > ルートxを含む式の積分公式 最終更新日 ∫ x d x = 2 3 x 3 2 C ∫ 1 x d x = 2 x C 目次 ルートxの積分 置換積分を用いる方法 分母にルートがある式の積分 部分分数分解の応用例 部分分数分解はいろいろな分野で使う基本的な計算方法です! 部分分数分解は,分数の和を計算するときに活躍します。 →分数で表された数列の和の問題と一般化 積分計算でも役立ちます。 →三角関数の有理式の積分分数関数の積分解法① 一見,分数関数の積分公式が使えないときの解法①は, (分子)÷ (分母)の割り算 をしてみることです。 分母が1次式,分子が2次式 のように,分母の方が次数が低いとき,この解法がうまくいくことがあります。
不定積分の計算(解析学A) (担当:高橋淳也) 1 不定積分の計算 ここでは,不定積分の計算方法を述べる.一般に初等関数の不定積分は初等関数で書けると は限らないが(例えば, ∫ e 2x dxは初等関数で書けない),特別な場合に初等関数で書け被積分関数の有理式を部分分数分解すると, とおける.右辺を通分するとその分子は, となるので, , , , とおいて解くと, , , , を得る.よって( 置換積分法で orj分母 (以前のプリント) ③ 分母が多項式で(分母の次数)<(分子の次数)( $ % 4 5 ④ 分母が因数分解可能 ( 部分分数分解 分数関数の不定積分 例題7) 次の不定積分を求めよ。
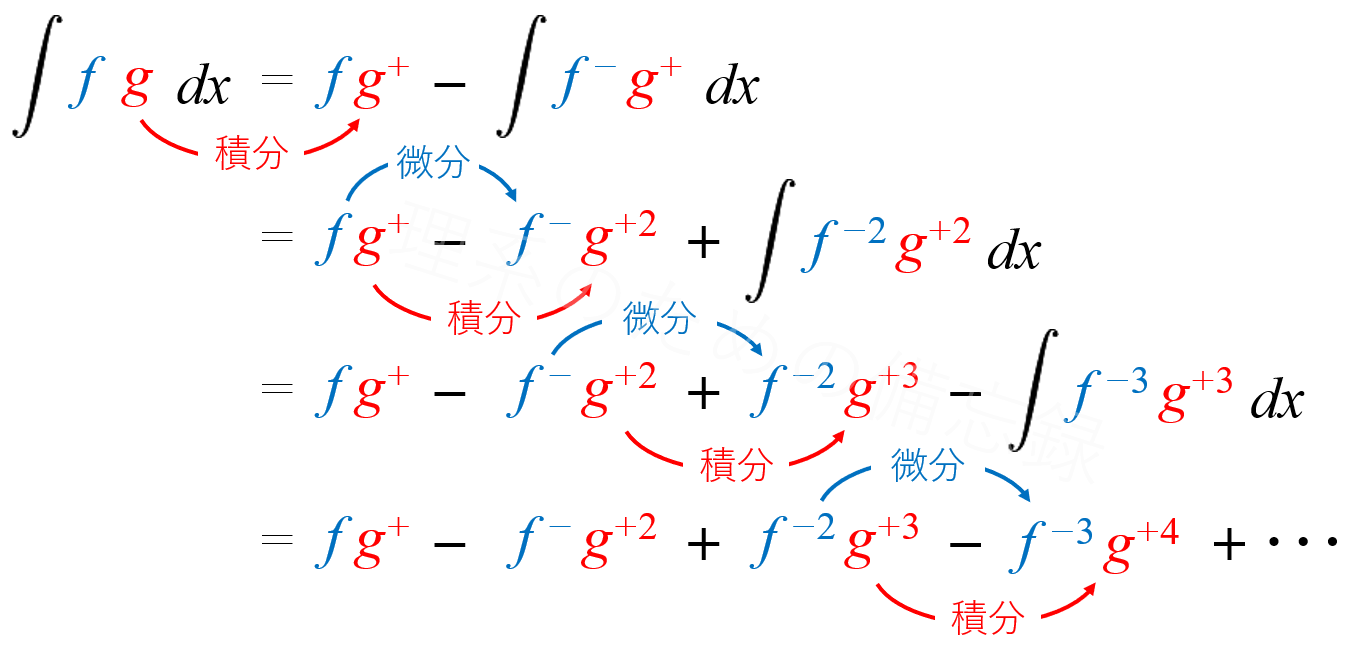



積分計算の便利ツール 瞬間部分積分 を使ってみる 理系のための備忘録



定積分の分母にxの二乗がある場合は どう計算したらよいのでしょうか 教 Yahoo 知恵袋
分数関数の積分の解法 Point:分数関数の積分 (1) 分子が分母を微分した式 のとき、 (2) 分子の次数 > 分母の次数 分子を分母で割った式より、分数式を分けて積分します。 例えば、 (3) 部分分数に分ける これらの式を用いて、部分分数に分けて積分します∫ 1 cos 2 x d x = tan x C;積分の計算のポイントをまとめると, 1.きちんと不定積分の計算ができているか ・・・微分して,正しいことを確認 3.分数・指数の計算は正しいか ・・・分数,指数,マイナスに注意 となります。気をつけましょう。




積分の基礎5 部分分数分解 Heavisideの方法 Youtube
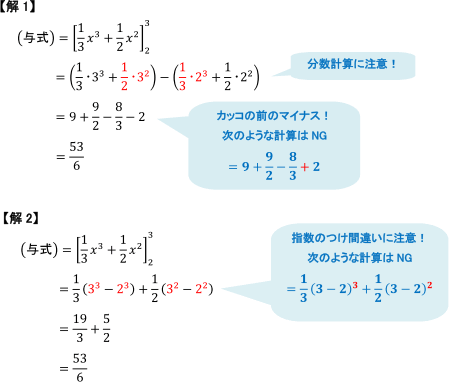



積分法 積分での計算ミスを防ぐポイント 数学 定期テスト対策サイト
分数関数の積分の公式 C は積分定数である。 C は積分定数である。 ∫ 1 x d x = log x C;積分計算の具体的事例 ここを見てください. 対数,三角関数,分数関数などの積分の例題を掲載している. ホーム>>カテゴリー分類>>積分 >>積分の計算手順 初版:04年7月1日,最終更新日: 13年6月11日 ページトップ 分数型の定積分その1 例題1 次の定積分を計算しなさい。 ∫ 1 0 x2 2x x3 3x2 2 dx ∫ 0 1 x 2 2 x x 3 3 x 2 2 d x 置換積分を学んだ後であれば、分母を別の文字で置いて、 u = x3 3x2 2 u = x 3 3 x 2 2 として考えようとする人もいるかもしれません。 このよう




積分での計算ミスを防ぐポイント 数学 苦手解決q A 進研ゼミ高校講座




高校数学 数 動画 分数関数の積分 の問題 19ch
1xn (x ≠ 0) 数学III で登場する多項式、分数関数、無理関数の不定積分は左の公式だけでは処理できず、部分分数分解、置換積分、部分積分などの公式も合わせて使う。 したがって、この頁を読むには部分分数分解、置換積分、部分積分などの項目を先にガンマ関数 定義4 p > 0に対して次の広義積分の値を対応させる関数(p)をガンマ関数という: (p) =∫ 1 0 xp 1e x dx 例題12 次の広義積分の値を求めよ.ただし,nは0以上の整数とする. (1) ∫ 1 0 1 (x2)(x4)dx (2) ∫ 1 1 1 x2 1 dx (3) ∫ 1 0 xne x dx 解答例 (1) 非積分関数を部分分数展開すると,b >本時の目標 置換積分により, \(\sqrt{x a}\) を含む無理関数の不定積分を求めることができる。 \(\displaystyle \frac{1}{\sqrt{1 x^2}}\) を含む不定積分を求めることができる。 \(u = x \sqrt{1 x^2}\) の置き換えにより, \(\displaystyle \int \frac{1}{\sqrt{1 x^2}} \,dx\) を求めることができる。




Taromath 分数関数 有理関数 の積分



分数関数の積分 高校数学 高校化学 高校物理に関連した基礎の基礎の復習です
tanを使った置換積分 先ほどの例題を、別の置換方法で見てみましょう。 例題 次の不定積分を計算しなさい。 ∫ 1 x√x2 1 dx ∫ 1 x x 2 1 d x ここでは、 x = tant x = tan t (− π 2 < t < π 2) ( − π 2 < t < π 2) とおいて計算してみることにしましょう。 この分数を求める 線形方程式 二次方程式 極限値 代数電卓 三角法電卓 微積分電卓 行列計算機 数学の問題を入力 解 代数 三角法 統計 微積分 1 分数関数の積分 11 パターン分け 分数関数は以下のパターンに限られます。 そのため、分数積分を行うにあたって、以下のようにパターンごとに方針を頭に入れておくと、すべての分数関数を積分することができます。 12 必要な道具




平方根内が2次式である関数の不定積分 身勝手な主張




高校数学 分数関数の積分 1 問題編 映像授業のtry It トライイット
有理関数の積分に部分分数分解を利用することができる。 有理関数の積分に ∫ 1 1 x2 dx = tan − 1x C を利用することができる。 分母が因数分解できるタイプの分数関数は,\ {部分分数分解}してから積分するのであった {1} { (t1)t}= {A} {t1} {B} {t}\ とおいて分母をはらうと 1=AtB (t1) t=1としてA=1,t=0としてB=1を得る 常にe^x>0より,\ 絶対値ははずせる 本問は圧倒的に簡潔な別解1を習得して分数を求める 線形方程式 二次方程式 極限値 代数電卓 三角法電卓 微積分電卓 行列計算機 数学の問題を入力 解 代数 三角法 統計 微積分




高校数学 分数関数の積分 2 問題編 映像授業のtry It トライイット




解析学基礎 基本的な積分 Wikibooks
2 無理関数とは 無理関数 •「変数と定数の四則演算」および「根号(平方根や冪根)」 によって表される関数. 例 (x2 2) √ 2 − 3x, 1 √ x, x2 3 √ x2 1, • 根号の中に少なくとも1つの変数を含まなくてはならない 例 x2 3 √ 2 は無理関数ではない (2/14)分数関数積分例題 TOP PAGE 大学別年度別入試問題目次 分野別入試問題目次 今週の名問 今週のダメ解答の解きなおし 京極一樹の入試対策書籍 現在販売中の最強入試対策書籍 御注文の手引き・割引 あなたは部分分数分解を単なる「式の変形」だと思い込んでいませんか? 実は数学b の数列の単元や数学3の積分計算でとてもお世話になる、大切な式変形なんです。 今回は、その「部分分数分解」を、公式・やり方だけでなく数列の問題への応用を詳しく解説しました!
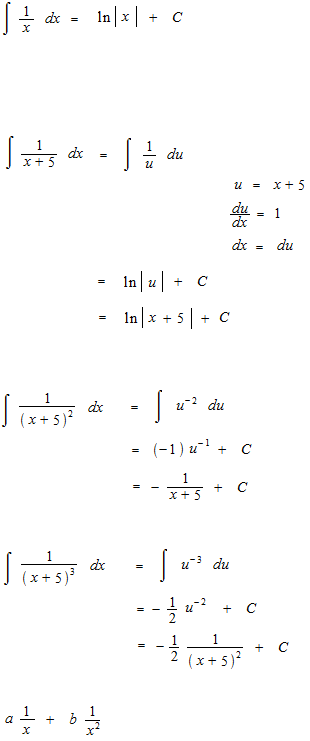



981 部分分数 Tokyomaths Com




大学の微分積分です 3 は何故この部分分数展開から始めると判るので 大学 短大 教えて Goo
分数関数の積分の計算方法 1 分子の次数が分母の次数より低くなるように 割り算を実行 しておく 2 分母が因数分解できるなら 因数分解して部分分数分解 する 3 分解したそれぞれは で計算できる (特に分母が1次式なら となる。 ) 4 定積分のとき この操作のことを「\(\dfrac{1}{4×5}\) を部分分数分解する」と言います。 微分や積分など、複雑な計算をするときは部分分数分解で「分数の足し算」に変形すると計算が楽になるケースが少なくありません。 部分分数分解をマスターすると、そういった複雑な計算でつまずく事がグッと分数式は必ず積分できる たとえば,$\frac{2x^8x^7x^6x^5x^45x^36x^26x4}{x^64x^56x^46x^33x^22x2}$の積分.(これなら誰も 読む気しない だろうw) まず,分子の次数が,分母より高ければ,割り算を行って,「多項式+分数」の形にする.



分数関数の積分 京極一樹の数学塾




H26版 赤チャート 数 P271練習240 ますいしいのブログ




3 タイプの 1次分数関数型の積分公式 Den Of Hardworking



3



分数関数の積分 京極一樹の数学塾



Logxの不定積分




まるで囲った4分の1はどこから来たのでしょうか Clear




高校 数学 積分法18 分数関数の積分2 19分 Youtube



東大数学専科典型題演習40 有理関数積分
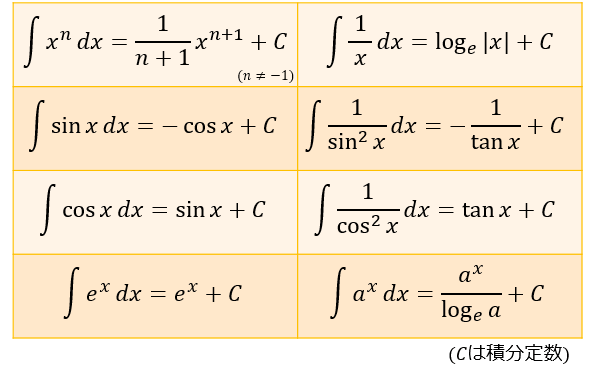



積分の公式一覧 アタリマエ



部分分数分解の公式とやり方を解説 Studyplus スタディプラス



数学iiiチェック リピート 第5章 1積分の計算 5 有理関数の積分 部分分数分解 Pukiwiki




数学 積分計算の型網羅part3 分数関数 理系ラボ




Log Xの積分計算の2通りの方法と発展形 高校数学の美しい物語




3番の問題について質問です 部分分数分解をする時に A X B X 2 C Clear



分数関数の積分について 合っているか添削していただけませんか 小さく Yahoo 知恵袋




部分分数分解の主要パターン おいしい数学




高校数学 見た目で分類した 数 数 の積分公式 解法集 Blastopore Note



分数関数の積分 京極一樹の数学塾



積分 1 Sinx
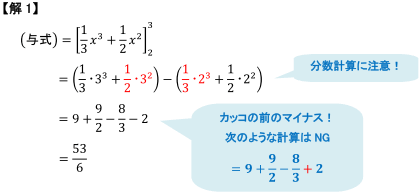



積分での計算ミスを防ぐポイント 数学 苦手解決q A 進研ゼミ高校講座
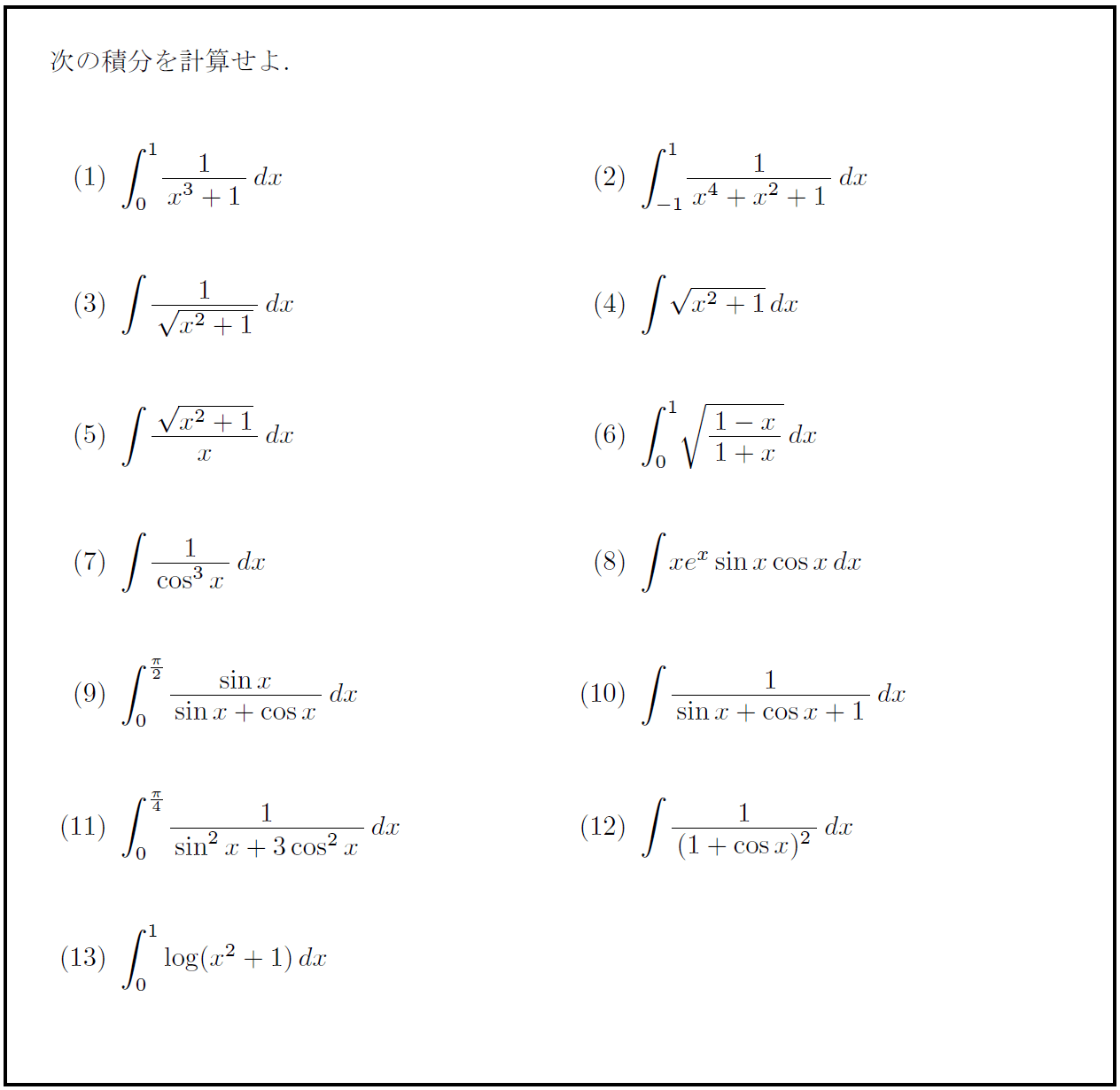



高校数学 高校生 受験生への挑戦状 積分最難問ランダム13題 受験の月




大学数学 有理関数の積分




有理関数の積分法 17 2 怜悧玲瓏 高校数学を天空から俯瞰する



48s96ub7b0z5f Net Chikansekibun Ouyou




高校数学 F X F X の不定積分 1 映像授業のtry It トライイット



数 不定積分 部分分数分解 オンライン無料塾 ターンナップ Okedou



Http Www Math Keio Ac Jp Miyazaki B1 1b17pb1 Pdf



分数関数の不定積分




うさぎでもわかる解析 高校数学 数3 Part05 部分分数分解を用いた積分 工業大学生ももやまのうさぎ塾




高校数学 これで完璧 整式の分数関数の積分 4つの手順 Youtube




数学 積分計算の型網羅part3 分数関数 理系ラボ




不定積分ですが ルートと分数が混ざると急にやり方が分からなくなりま 高校 教えて Goo




積分 逆双曲線関数 何度も置換を乗り越えて No 049 衒学記鳥の日樹蝶
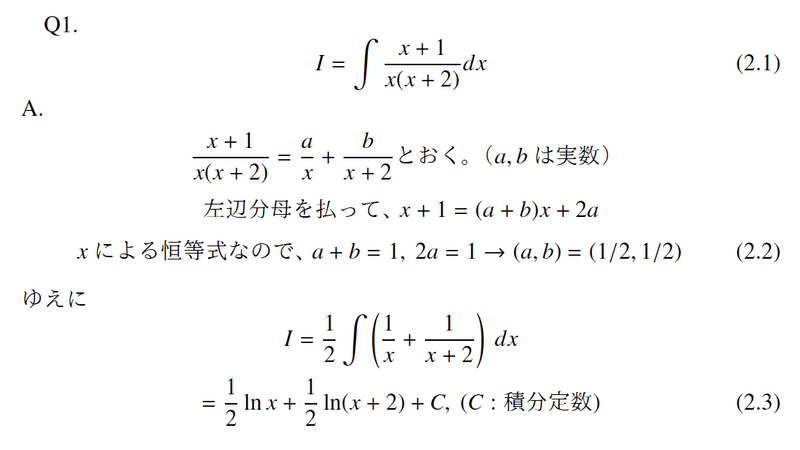



文字起こし 数学って難しい Notebook70 Note



分数関数の積分 京極一樹の数学塾
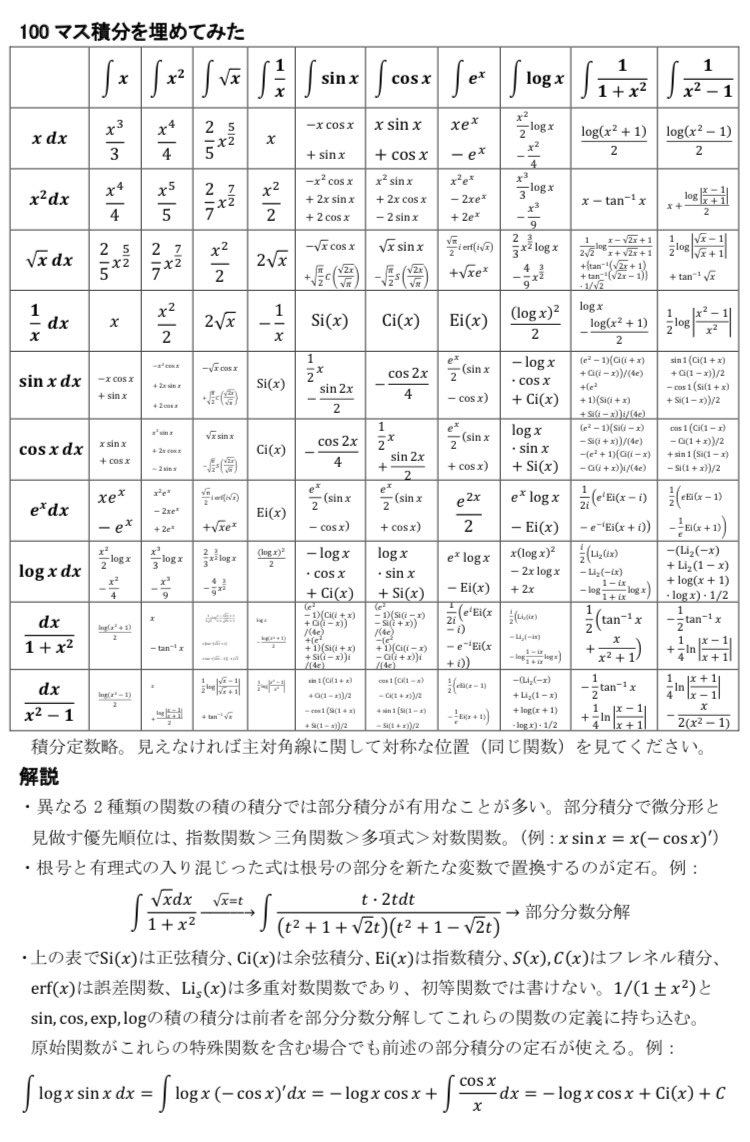



佐久間 100マス積分を埋めてみた 被積分関数が簡単な関数の積なので 下に書いてある定石通りに部分積分すれば 部分分数分解は面倒臭いけど 全部できる イオン化傾向みたいなノリで 微分形見做され傾向 を掴もう 答えに特殊関数が現れないものは大学




解析学基礎 基本的な積分 Wikibooks




置換積分の公式と例題 三角関数sin Tanを使ったパターンの解き方 アタリマエ



Http Math Cs Kitami It Ac Jp Kouno Kougi Bi05a Kaisetu12 Pdf



Q Tbn And9gctb1ubqu Ih4gchq5l77k2yfsxuuemlw Sp8vyawtal 9fl1ix Usqp Cau




北大数学理系前期第5問 大学受験in北海道




置換積分の方法 置換方法を覚えておきべき積分問題 大学入試数学の考え方と解法




すん Syn Dx はぅんsometimesはぁん Ayn With Bose Yobinori ヨビノリさん 今週の積分の別解です 三角関数未履修だったのでt X 1で置換したあと直感に従って部分分数分解しましたヽ ノ



三角関数の積分 京極一樹の数学塾



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




数学 分数関数の積分のやり方とコツ 教科書より詳しい高校数学



Http Www Enjoymath Sakura Ne Jp 1 Z Hansha Sekibun015teisekibun Bunsuu Kansuu11 C Utf8 Pdf




Excel Vba を学ぶなら Moug モーグ 即効テクニック 分数 根号 積分記号を入力する




ここの部分分数分解の仕方がわかりません よろしくお願いします Clear




うさぎでもわかる解析 高校数学 数3 Part05 部分分数分解を用いた積分 工業大学生ももやまのうさぎ塾




数学 積分計算の型網羅part3 分数関数 理系ラボ



分数関数の不定積分



分数関数の不定積分




1 Xⁿ 1 を積分する 部分分数分解 理系のひとりごと




数 141 分数関数の積分 Youtube




分数関数の積分 数学の偏差値を上げて合格を目指す




数学 積分法 怜悧玲瓏 高校数学を天空から俯瞰する




有理関数の積分 小西研究室 電脳工房msc Atwiki アットウィキ



三角関数の積分 京極一樹の数学塾




置換しないで積分したい積分問題 大学入試数学の考え方と解法




高校数学 置換積分法 1 問題編 映像授業のtry It トライイット



1




高校数学 分数関数 有理関数 の積分2パターン 分子の次数下げと部分分数分解 受験の月



分数関数の不定積分なのに 1 2がなぜないのですか Yahoo 知恵袋




数学 分母が3次までの部分分数分解の公式 全6パターンの解法紹介




部分分数分解のやり方のコツ 公式と応用までわかりやすく解説




数学 For 大学受験 على تويتر 解答 積分で表された方程式だし 微分したくなる気持ちを抑え なんか違う方法ないかなあと考えていると 分数を分ける方が楽だということに気付いた もちろん定石通り 微分しても解けるが めんどそうだったのでやってない



分数関数の不定積分




高校数学 無理関数の積分2パターン 分母の有理化と根号丸ごと置換 受験の月



不定積分とは 公式や計算問題の解き方 分数を含む場合など 受験辞典
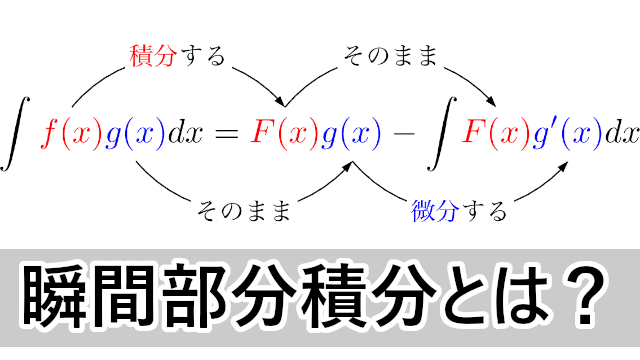



面倒な部分積分を 瞬間部分積分 で簡単に求めよう 大学入試数学の考え方と解法
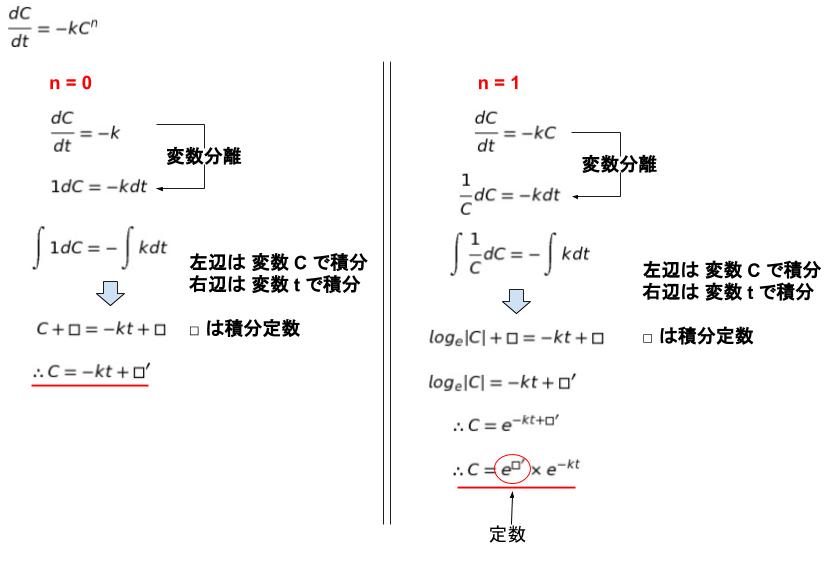



微分方程式 薬学 これでok



部分分数展開を利用した積分




高校数学 分数関数の積分 2 問題編 映像授業のtry It トライイット




1枚目の部分積分は分数でない形にしてから計算しないといけない一方で 2枚目 3枚目は Clear




積分 X 1 パターン 完成図の予想 No 021 衒学記鳥の日樹蝶




数 不定積分 部分分数分解 オンライン無料塾 ターンナップ Youtube



高校数学 指数関数の積分 最悪e X Tとおけ 受験の月



分数関数の不定積分




数 不定積分のまとめと解き方 Part8 関数の商の積分 解法まとめ すうじょうさん Note




部分分数分解と有理関数 三角関数 無理関数の不定積分



分数関数の積分で4分の1が出てくる理由が分かりません 教えて下 Yahoo 知恵袋




積分 置換積分 何をtとおく 数学の偏差値を上げて合格を目指す



3



48s96ub7b0z5f Net Bunsuukansuu Sekibun




分母が二次式の積分 理系ノート




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ



三角関数の積分 京極一樹の数学塾



置換積分法とは 公式やパターンを見抜くコツ 三角関数 ルートなど 受験辞典



0 件のコメント:
コメントを投稿