正六角形がイラスト付きでわかる! 全ての辺と角が等しい六角形。 概要 六角形における正多角形。内角は1°。 単独で平面充填が可能な正多角形全3種の内の1種。 中心と各頂点とを結ぶと6つの正三角形が現れる。 これは「中心と頂点との間の距離」と「辺の長さ」とが等しい事を意味し1/7/14 正多角形の性質 正九角形を例に YouTub (1)十角形の内角の和を求めなさい。 (2)正十二角形のひとつの内角の大きさは何度ですか。 (3)角形の外角の和は何度ですか。 (4)十五角形の対角線の本数は何本ですか。 正多角形に関する公式 まずはこうL02/03正多角形の1つの内角/外角 p1 l041つの内角→正多角形 p2 l05対頂角 p3 l06/07平行線の同位角/錯角 p4 l08平行線の間の角 p4 l09二等分線と角 p5 l10
実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note
正多角形 外角
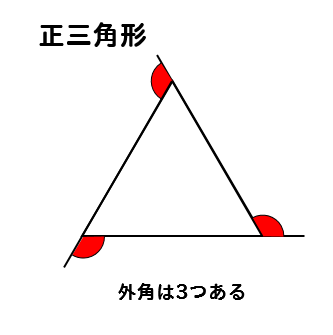
正多角形 外角-正二十角形においては、中心角と外角は18 で、内角は162 正多角形を作るには 1 次の問いに答えなさい。 (1) 角度が100 より大きい\xがある。この\xを1 つの内角とする正多角形を作ろうとしたら, 作ることができなかった。\xの大きさを2 種類求めよ。角というのは、直線や線分が交差した点と、その両端の線で挟まれた部分のことを言います。 多角形はどのように区別がされているかというと、この角の数によってされています。 左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足すと 180° になり



Q Tbn And9gcraxa oxo33qx3gflo Kiznbdkfkey3w9pf8 Qzhktmhwurkr Usqp Cau
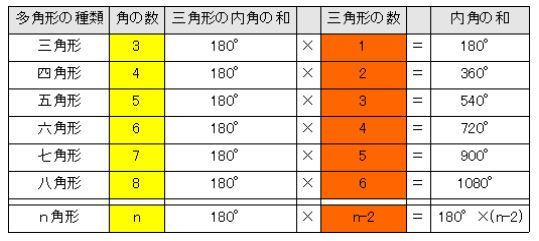
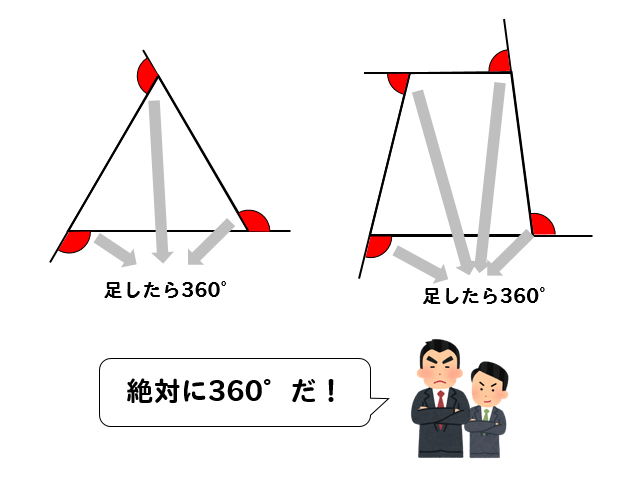
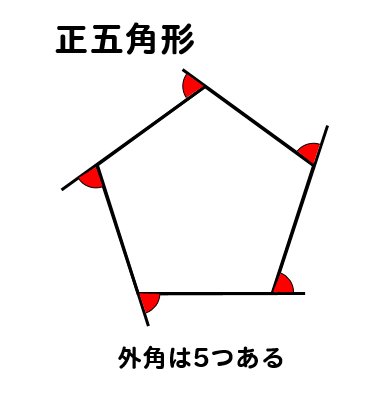
多角形の内角の和・外角の和 三角形・四角形・五角形・など、 頂点が 3 3 つ以上の角ばった図形のことを「多角形」と呼びます。 内角の和は540度です。すべての辺の長さが等しく,すべての内角の大きさが等しい多角形を正多角形という 正多角形の1つの 外角 の大きさは 正多角形の1つの 内角 の大きさは多角形の外角の和が360°になることの説明。 まず四角形で考えてみましょう。 図に示した赤い角度が外角です。さらに内角を青で表示します >>内角 内角と、それに隣り合う外角の和は180°です。図では隣り合っている赤と青のそれぞれが1組180°です。
• 多角形の外角の和は 360° 正多角形のすべての内角の大きさは等しく,すべての外角の大きさは等しい したがって,正n角形の1つの外角の大きさは •外角の大きさの公式の説明 正多角形の外角の大きさが、 $\dfrac{360}{n}$ という公式で計算できることを証明してみましょう。 公式の証明1 一般に 多角形の外角の和は $360^{\circ}$ です。 だから、正多角形の1つの外角の大きさは、 (多角形の外角の和)÷ n = 360°/n になるんだ。 ただ公式をつかうだけじゃなくて、 なぜ、使えるのか?? ってこともおさえておこう! まとめ:正多角形の外角の大きさはたまーにでてくる! 正多角形(n角形)の大きさは、 360°/n で計算で
正六角形(正6角形)の角度の求め方は?内角の和、外角 正六角形(正6角形)の1つの角度は1°です。正六角形(正6角形)の内角の和は、 180°×(n-2) =180°×(6-2) =180°×4=7° 内角の和、外角の求め方は下記が参考になります。 多角形の内角の和は?正9角形だと思われます 内角が140° つまり外角は40° 多角形の外角の和は360°となるので、360÷40=9 つまり、正9角形では無いでしょうか? 間違えてたら、すみません19/2/21 (2) 多角形の外角の和の公式より、 多角形の外角の和は、常に \(360^\circ\) であるので、 正九角形であるとき、\(1\) つの外角の大きさは \(360^\circ \div 9 = 40^\circ\) 答え: \(40^\circ\) (3) 多角形の対角線の本数の公式より、 \(\displaystyle \frac{n(n − 3)}{2}\)



多边形的外角内角度数计算公式 正多边形外角度数公式 公式学习



内角攻め それとも外角攻め すうがくラボのブログ
Xyz= ° スフ点 ス ス ス ス Help スO スp ス` スフ難ソスp スフ和 ス ス180° ス ス ス ス ス ス ∠a∠b∠c=180° スe スX スフ難ソスp, スO スp スフ組 スヘ対抵ソス スp ス ス ス ス ス逑呻ソス ス ス ス ∠x=∠a ∠y=∠b ∠z=∠c ス艪ヲ ス ス,上の事実は次のように説明できます. まず, 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので, n n 角形の内角と外角の和の合計は, 180°×n 180 ° × n です.そして, n n 角形の外角の和は,これから内角の和をひいたものなので, 180ウチダ 教材総合カタログ 小学校 >> P5 発表・表示用教材 (図形)図形説明器具A (説明器 (多角形)・図形描画ソフト) 正多角形プログラミング作図指導シートScratchを使った正多角形の作図の指導におススメ!目安1校あたり1程度小5年算振2マグネットシート




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




高中数学知识点 多边形外角和等于360 动画版 每日头条
↓ ↓ ↓ ↓ ↓ ↓https//studyline32com/l/u/6XQOiYkgoDeSmFNm中2で学習する図形の単元から「正多角形の1つの内・ 多角形の外角の和を利用し,様々な多角形の外角の大きさを求めることができる。 4 本時の評価規準 評価規準(評価方法) A:十分満足できる B:おおむね満足できる 数学への関心・意欲・態度 多角形の外角の和について 多角形の外角の和を求めよこの性質は多角形、正多角形に関係なく どんなやつでも全部合わせたら360°になります。 では、このことを使って考えると 正多角形の外角1つ分の大きさは $$\LARGE{360 \div (角の数)}$$ をすることによって求めることができます。 正三角形の場合




正多形的外角 搜狗搜索




一看就懂的视觉证明2 多边形外角和 哔哩哔哩 Bilibili
多角形の外角の和 内容 n角形の外角の和は、360°である。 証明 三角形の場合 三角形の一つの外角は他の2つの内角に等しいので、外角の和は、内角の和を2回足したことになるので三角形の外角多角形の角度1 名前 次のそれぞれの問いに答えなさい。 正五角形の内角の和を求めなさい。 式 正二十角形の1つの内角の大きさを求めなさい。 式 1つの外角の大きさが40°であるのは正何角形か。 式 1つの内角の大きさが1°であるのは正何角形か。 式「正多角形」の意味や性質を理解する。 円の中心の周りの角を等分して正多角形をかく方法を理解する。 円の半径の長さを使って正六角形を作図し,正多角形と円の関係について理解を深める。 (本時




内角の和が2340度である正多角形の一つの外角の大きさを求める問題の答えが24度なん Clear



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
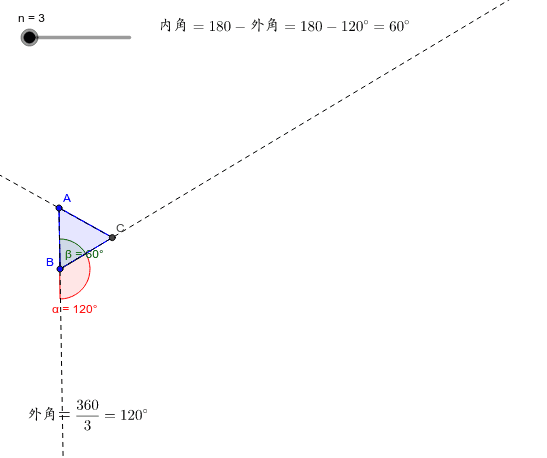
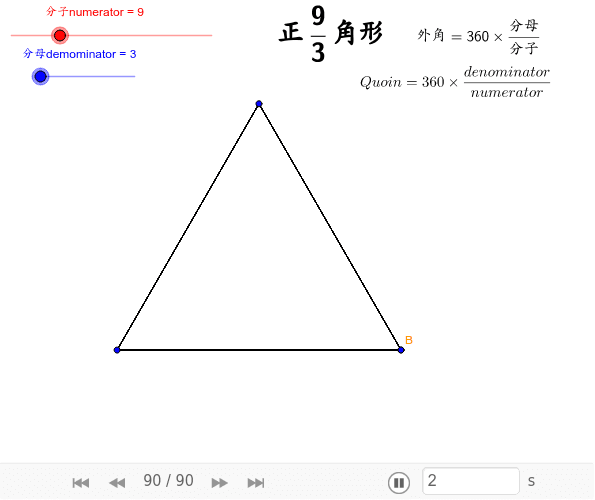
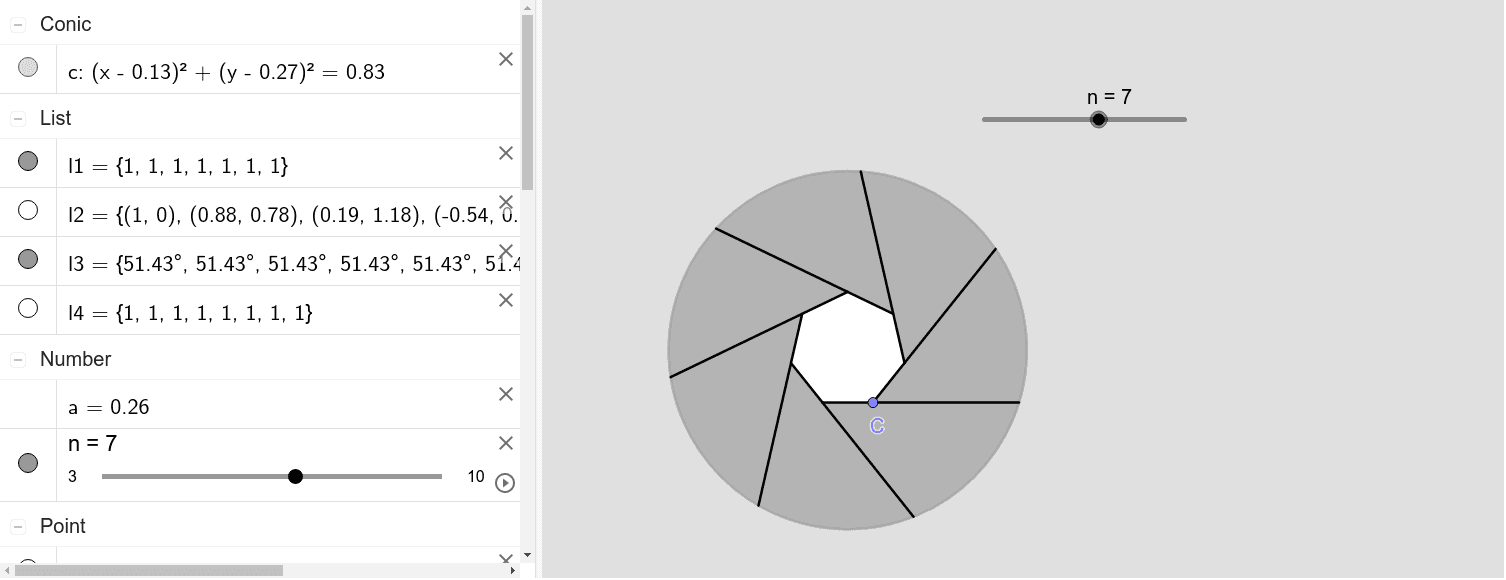
これは多角形の外角の和の研究です。 多角形の内角の和は変化しますが、外角の和は一定です。 つまり、内角の和の公式よりも、外角の和の方が本質的だということです。 それを直観的に証明してみましょう。 そして、このことから、外角から正多角形を作ることができます。ここで分数の正多角形とは何かを考える。 まず、正五角形の外角は 360 ° ÷5で72°で あるが、正5/2角形の外角は 360 ° ÷( 5/2 )で144° となる。では 正5/3角形はどうかを考える。図8 は正五 角形の外角を表わし、図9は正5/2角形の 外角を表わしている。図10は正5/3角形正多角形の重心は最長の対角線どうしの交点(正 2n 角形に限る)や外接円および内接円の中心に一致する。 正多角形は、角(辺)の数が増えるごとに 円 に近づいていくので、「周の長さ÷ 外接円 の 直径 」を角の数が多い正多角形で計算すると、 円周率 に近づいていく。




多角形の内角の和 外角の和の公式 数学fun



正五边形abcde中 你会求 m的度数吗 陕西中考数学真题 多边形的内角和公式 外角和公式 哔哩哔哩 つロ干杯 Bilibili
正多角形の外角の和って360度ですね。 という事は、正三角形の一つの外角は360÷3 正方形の一つの外角は360÷4 正五角形の一つの外角は360÷5 というようにしていけば正多角形の内角と外角 次の問に答えなさい。 ⑴ 正十角形の1つの内角の大きさを,下の①,②の2通りで求めた。 〔 〕にあてはまる数を書きなさい。正六角形の1つの内角の大きさを求めなさい。 式 答え 正八角形の対角線の数を求めなさい。 式 答え 1つの外角の大きさが°であるのは正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え 内角の和が °であるのは、正何角形か。 式 答え




360影视 影视搜索




01 004 基础数学之平面几何知识点精讲汇总 多边形 简书
正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 正多角形は線対称の図形であり、正 n 角形に対称軸は n 本ある。 また、正偶数角形は点対称の図形でもある。 辺の数が同じ正多角形どうしは全て互いに23/9/15 正多角形の1つの内角の大きさを出したいときは、 内角の和を頂点の数でわればいいんだ。 内角の和「180°×(n2)」を、 頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。 180× (n2)/n どの内角も同じ大きさだからね! まとめ:正多角形の内角は「総和」を「頂点の数」でわれ! 正多角形の内角の公式は、



Q Tbn And9gcraxa oxo33qx3gflo Kiznbdkfkey3w9pf8 Qzhktmhwurkr Usqp Cau




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊




内角正多边形外角定理png图片素材免费下载 图片编号 Png素材网



1



初中数学多边形内角和 掌握一个公式 学会内外角结合求解边数



正多边形的内外角和定理及其性质在中考中常考 解决这类题目需要掌握正 一家家教育网



一看就懂的视觉证明2 多边形外角和 哔哩哔哩 Bilibili



正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊




09多边形的外角和平行四边形初中数学初二 Youtube




八年级数学下册第六章平行四边形6 4多边形的内角和与外角和6 4 2多边形的外角和课后作业新版北师大版下载 Word模板 爱问共享资料



正多边形每个外角公式 正多边形外角和 七月seo



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




ひとつの外角が40度の正多角形は正何角形かどう求められますか 教えてください Clear




正多角形の内角と外角の大きさ 具体例で学ぶ数学




多边形的内角




コンプリート 多角形角度公式 ニスヌーピー壁紙




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



多边形外角和等于360 的一种直观解释 Matrix67 The Aha Moments




R3maova8nqwrcm



正多角形の外角と内角 Geogebra



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊



多边形的角 禾教 初中数学互动课堂




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



若一个正多边形的一个外角是45 则这个正多边形的边数是 X题卡



正五边形的外角和等于多少度 初三网



正多边形的外角 多边形的内角和与外角和同步练习 带答案 尚书坊



五边形有几个外角正五边形外角和多少度 天奇生活



9 2 多边形的内角和与外角和 Page 华师大版七年级数学下册电子课本 教材 教科书 好多电子课本网



初中数学已知外角求正多边形的内角和难住不少同学 记住这点秒杀 哔哩哔哩 Bilibili




09多边形的外角和平行四边形初中数学初二 Youtube



正多边形内角和多边形内角和公式推导方法 尚书坊




正多边形每一个外角 搜狗搜索




李志鹏 古晋三中 分享我校数学教师陈俊益老师讲解初二数学第五章之外角和的教学视频 古晋三中 线上教学




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和の公式 数学fun




正多形的外角 搜狗搜索



正多邊形的內角與外角 Live 多媒體數學觀念典online




正多角形の1つの内角 外角を求める方法を問題解説 数スタ



1



2 三角形的内角与外角和 Page76 华师大版七年级数学下册电子课本 教材 教科书 好多电子课本网



一个多边形的每一个外角都等于30 这个多边形的边数是 它的内角和是 度 初中 数学试题 多边形的内角和和外角和考点 好技网




正多边形一共有多少个



正多边形的边数公式 西瓜视频搜索



多边形的内角和 三角形ppt 第一ppt




十六边形外角和 搜狗搜索



五边形有几个外角正五边形外角和多少度 天奇生活



初二数学 一个正多边形内角和为1080 则每个外角度数为多少 哔哩哔哩 Bilibili



分数正多角形 Fractional Regular Polygon Geogebra



光圈与正多边形外角和 Geogebra



1




多边形的内角




内角の和 180 N 2 外角の和 360 教遊者




正五边形的外角和是多少度



正多边形每个外角公式 正多边形外角和 七月seo




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




正多角形の1つの内角 外角を求める方法を問題解説 数スタ



多角形の外角の和 On Vimeo
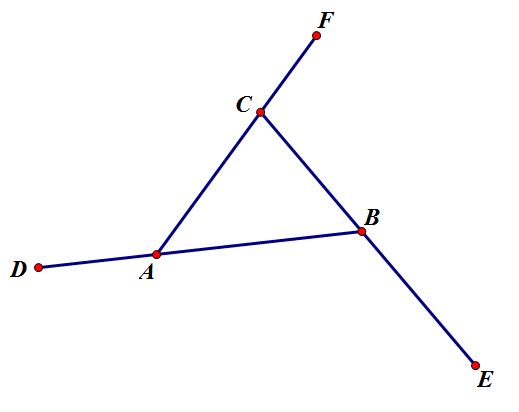



求多边形外角和的绝妙方法 科学空间 Scientific Spaces




七年级数学检测 Doc 文档分享网
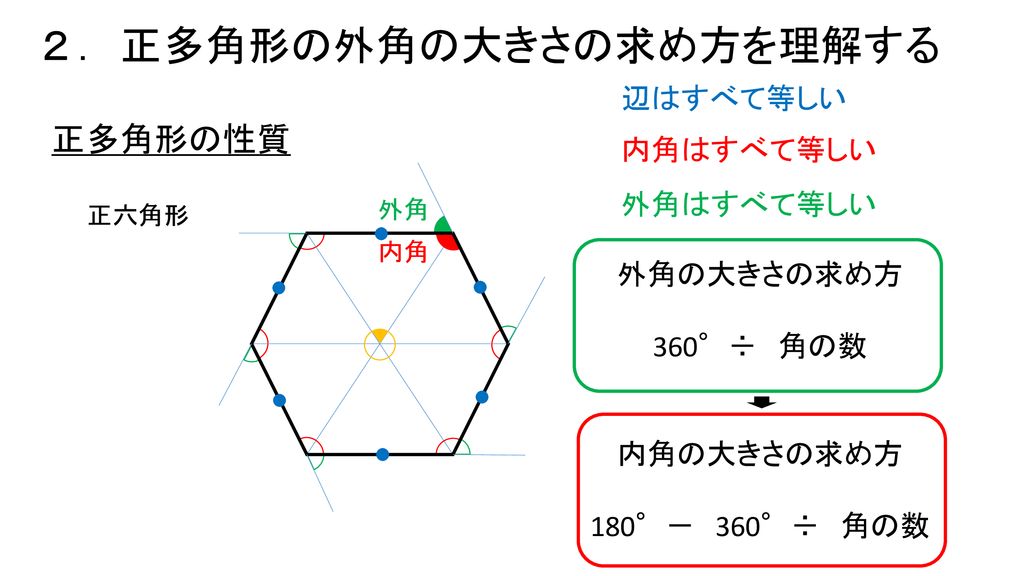



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




小学校5年 算数 正多角形の角の大きさ Youtube




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




多边形内角和和外角和 简书



多边形的内角和与外角和 Ppt课件 第一ppt
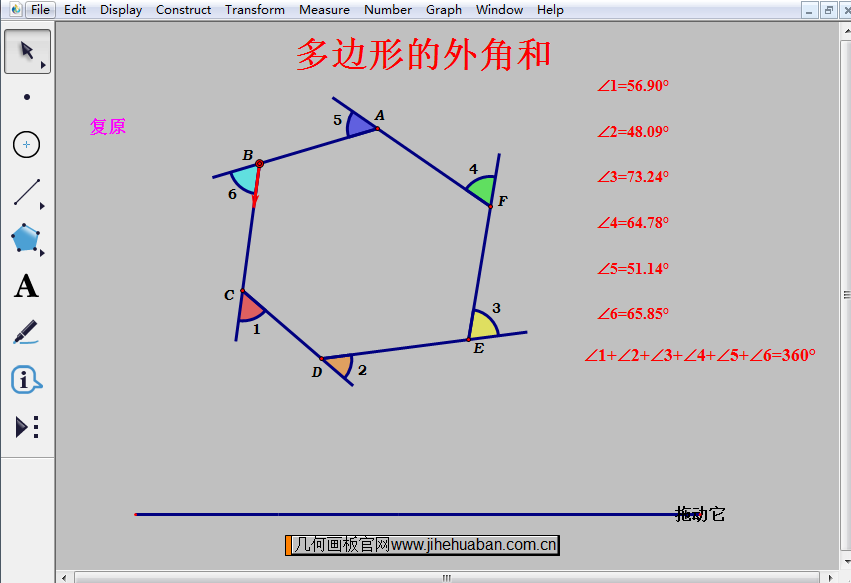



几何画板动态演示多边形的外角和




コンプリート 多角形角度公式 ニスヌーピー壁紙



多边形的内角和与外角和 平行四边形ppt 第2课时 第一ppt




內角和外角 维基百科 自由的百科全书




如何利用编程机器人程小奔编程玩几何 Makeblock
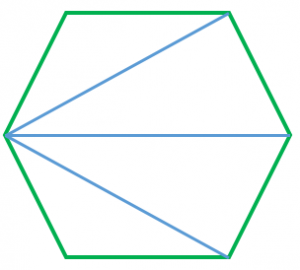



正多角形の内角と外角の大きさ 具体例で学ぶ数学



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




正多边形内角和公式及定义 快资讯



怎么算多边形外角和 西瓜视频搜索



多边形的角 禾教 初中数学互动课堂




中考重头戏 多边形到圆 极致到完美 每日头条



正多边形内角外角公式 正多边形外角度数公式 七月seo



正多边形外角和公式 初三网




360影视 影视搜索




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



多边形的内角和与外角和 平行四边形ppt 第2课时 第一ppt




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



腾讯视频



正多角形の内角と中心角 家紋の描き方007b 夏貸文庫



多边形内角和定理 快懂百科



一个多边形的每一个外角都等于30 这个多边形的边数是 它的内角和是 度 初中 数学试题 多边形的内角和和外角和考点 好技网



正多边形内角外角公式 正多边形外角度数公式 七月seo



0 件のコメント:
コメントを投稿